How do falling cats always manage to land on their feet? It is a puzzle that seems like it should be easy to answer with modern physics, but it took a surprising amount of time for physicists to solve the mystery – and there are still things we can learn from the falling cat problem today.
Research into the physics of the cat’s ability – often referred to as the cat-righting reflex – is almost as old as physics itself.
The first research paper to tackle the subject was published in the year 1700 by a French scientist named Antoine Parent. For context, Isaac Newton was still alive at the time and his groundbreaking physics work Philosophiæ Naturalis Principia Mathematica was only 13 years old.
Parent’s interests were far from feline falls: he was investigating how buoyant objects move and rotate while sinking to an equilibrium position. Almost as an afterthought, Parent suggested that, just as a weighted object might flip heavy-side-down in water due to the clash of gravity and an upward buoyant force, a cat in freefall might adjust its spine to flip itself over, moving its centre of gravity above the centre of buoyancy.
Read more about cats:
This idea was wrong, as the buoyant force of air is far too weak to affect a cat in a typical fall. Yet this explanation, and diluted versions of it, remained common in popular books on cats through the mid-1800s. The image of the cat was undergoing a rehabilitation in the United Kingdom at that time, and Parent’s hypothesis appeared in texts that mainly described the best way to care for and pamper one’s beloved feline friends.
The physics community, however, had moved on to new explanations. In the early 1800s, there was a growing recognition that certain fundamental quantities in nature are conserved in any physical process.
Most people are familiar with the conservation of energy, the recognition that energy is never created or destroyed, only converted into different forms. For example, a car is set into motion by the conversion of chemical energy in the gasoline into mechanical motion of the wheels; the car is stopped when the brakes are applied, converting the motion of the car into heat energy through friction.
Physicists had also long recognised that momentum is conserved in any physical process. For a single object in motion, momentum is the product of mass times speed, and heavier and faster objects have more momentum than light and slow ones.
By the mid-1800s, another conservation law had been recognised: the conservation of the momentum of rotation, or angular momentum. An immediate consequence of this law is the observation that it is not possible for one object to begin rotating without another object rotating in the opposite sense, with the same magnitude of angular momentum.
It is easy to see this, approximately, in an ordinary spinnable office chair: if you twist your body suddenly to the left, the chair counter-rotates to the right.
Read more about physics:
- The weak nuclear interaction: the enigmatic fundamental force that makes life possible
- The parallel worlds of quantum mechanics
With the recognition of conservation of energy, physicists soon decided that a cat simply cannot flip over on its own in freefall once it begins falling. The consensus view was that a cat, at the moment it begins to fall, must push off of its perch to give itself some initial rotation that leads to it ending on its feet. The cat generates its angular momentum by imparting the opposite angular momentum to its perch and, consequently, the Earth itself.
But this explanation was demolished in a fateful meeting of the French Academy of Sciences on October 22, 1894, by the physiologist Etienne-Jules Marey. Marey presented a sequence of high-speed photographs taken of a falling cat, the first of their kind, showing clearly that the cat begins falling upside-down without any rotation but nevertheless manages to turn over to land on its feet.
The revelations of the photographs threw the meeting into disarray. One member of the Academy declared that Marey “had presented them with a scientific paradox in direct contradiction with the most elementary mechanical principles.”
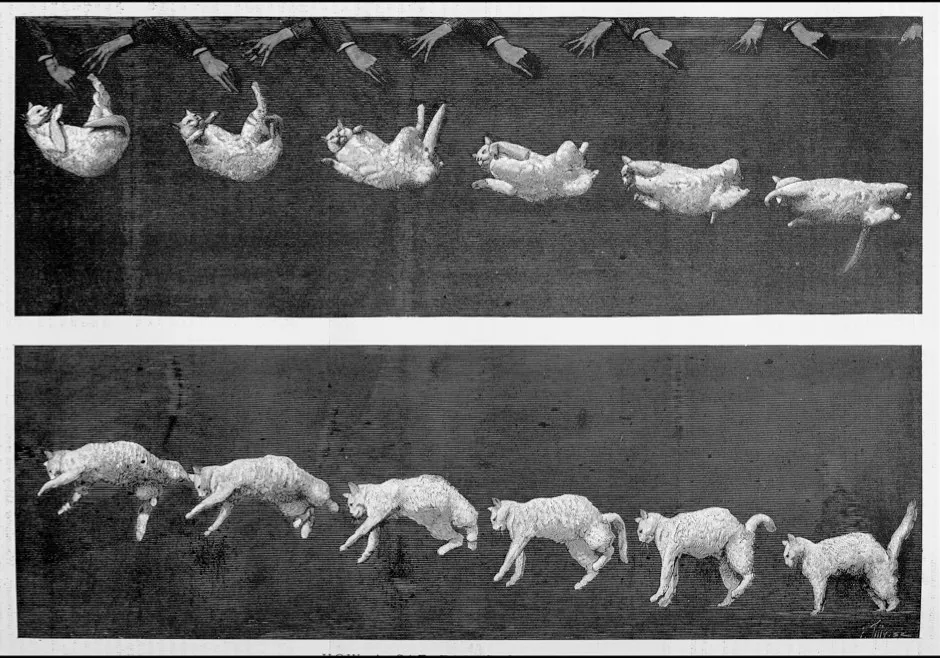
Where had the scientists gone wrong? They had succumbed to the adage that “a little knowledge is a dangerous thing.” Physicists, having newly recognised the conservation of angular momentum, had focused their attention on the study of rigid rotating bodies, like a bicycle wheel or a spinning planet.
A cat, however, as most cat parents can attest, is very far from a rigid body. Cats can bend, twist, and generally play different parts of their body off of each other to achieve a net rotation, even without angular momentum.
How do cats really land on their feet?
To their credit, physicists recognised their mistake very quickly, and proposed several mechanisms by which a cat might be able to right itself using different manipulations of its body parts. But the most important of these mechanisms was introduced by Dutch physiologists G.G.J. Rademaker and J.W.G. ter Braak some many years later, in 1935.
Read more about science history:
- Dragon breath, vomiting slugs and pigeon remedies: 8 bizarre medical stories from history
- Ada Lovelace: a mathematician, a computer scientist and a visionary
By this time, the question of cat-righting had been taken up by brain researchers. They wanted to understand which portions of the cat’s nervous system control the righting reflex. Rademaker and ter Braak helped to answer these questions, but in the process found existing explanations for the physics of cat-righting unsatisfying, and they constructed their own.
They imagined the cat as fundamentally consisting of two cylinders, representing the front and rear halves of the feline. If the cat bends at the waist, it can then twist the two halves of its body in opposite directions, causing their opposing angular momenta to largely cancel.
When it unbends, its body will be oriented in a different direction, even though the cat had no angular momentum to start with. This motion, now known as the “bend-and-twist” model of cat-righting, is arguably the most important movement that a cat undertakes to turn itself over.
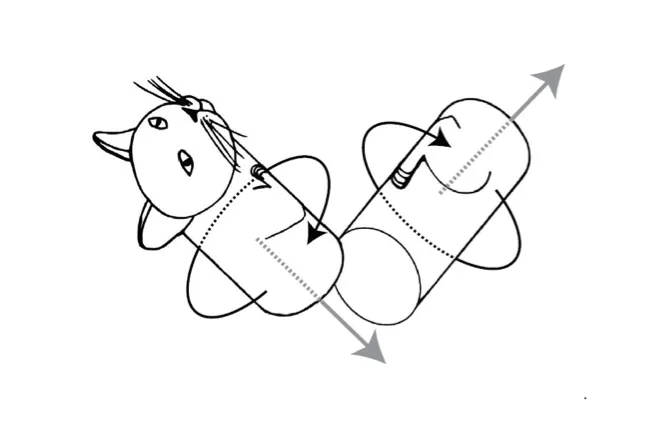
But investigations into the physics of falling felines did not end there. Rademaker and ter Braak presented only the simplest model of a turning cat. It captured the essence of the motion but not the details.
What can we learn from falling cats?
In the late 1960s, the problem again became of interest because NASA wanted to teach its astronauts how to turn over when in a weightless environment. This time, engineers at Stanford University took up the challenge, and they used computer simulations to refine the Dutch physiologist’s simple model. It is unclear if any astronauts actually attempted to perform this refined “bend-and-twist” in space.
Today, research into cat-turning continues in yet another field of study: robotics. Roboticists have long used nature as an inspiration to build better robots, and the falling cat provides a strategy by which a falling robot could land on its feet, minimising any damage it might otherwise suffer. Prototypes of falling robot cats have been created, but none have been made yet that can adapt to land on its feet from any starting position.
So how does a cat land on its feet? It turns out that the answer is complicated! Though “bend-and-twist” is the most important part of the cat’s manoeuvre, it clearly uses several different motions to turn as quickly and efficiently as possible. Though physicists often look for the simplest solution to a physical problem, nature looks for the most effective one, regardless of how complicated.
The instinct of physicists to look for simple solutions still leads to arguments. In response to a recent scientific paper I submitted on the mathematics of cat-righting, one reviewer argued that the “bend-and-twist” model must be wrong because he had watched a Youtube video of a falling cat and it didn’t look like it was moving in that way!
Cats are well-known for being keepers of secrets, and their righting reflex remains a mystery to many scientists to this day.
Falling Felines and Fundamental Physics by Gregory J Gbur is out now (£18.99, Yale University Press).
