How can I break an encrypted text? You’ve come to the right place! The purpose of this book is exactly to help you with this question. We'll first explain how to solve a substitution cipher, then how to work out what sort of encryption your text uses.
How to solve a substitution cipher
Let’s take a look at this cryptogram, an encrypted advertisement published in the London newspaper The Times on 1 August 1873. This, and some other encrypted newspaper ads we will be referring to later, are from Jean Palmer’s 2005 book The Agony Column Codes & Ciphers (Jean Palmer is a pen name of London-based code-breaking expert Tony Gaffney):

Here’s the text written in a more readable way:
HFOBWDS wtbsfdoesksjd ji ijs mjiae (dai ditwy). Afods ks rofed dpficqp licqp. Toeqfwus yic lsrd vspojt uwjjid qsd ibsf. Aoll sjtswbicf di edwy apsfs yic lsrd ce doll O pswf rfik yic, qobs yicf wtbous. Yicf cjpwhhy aors jid asll.
As a first step, we count the letters in the message (this is called frequency analysis):
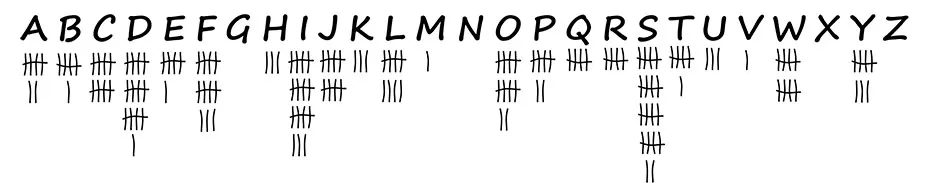
As can be seen, the letter S is the most frequent. It probably stands for the E, which is the most frequent letter in virtually every English text. After E, the letters T, A and O are the next most frequent ones in the English language, but it is difficult to identify these based on their frequencies alone.
However, there is another letter we can easily guess by looking at the ciphertext: the word ‘O’ must stand for ‘I’, as there is no other word in the English language that consists of only one capitalised letter (unless it is at the beginning of a sentence, in which case the letter ‘A’ would fit).
Further analysis shows that the text contains the word ‘yic’ three times and the word ‘yicf’ twice. The words ‘the’ and ‘them’ would be a good guess, but the letter ‘e’ has already been identified. So, ‘you’ and ‘your’ make sense.
Read more about codebreaking:
- Are you an expert codebreaker?
- Alan Turing’s legacy should be for his triumphs, rather than his tragedy
Knowing the ciphertext equivalents of the six letters E, I, Y, O, U and R, it is easy to guess more words. For instance, ‘ijs’ decrypts to ‘o?e’ (with the question mark standing for an unknown letter), which can only mean ‘one’. In the end, we receive the following plaintext:
PRIVATE advertisement no one knows (two today). Write me first through lough. Disgrace you left behind cannot get over. Will endeavour to stay where you left us till I hear from you, give your advice. Your unhappy wife not well.
If we can use a computer and a program such as CrypTool 2 (free open-source software available at cryptool.org), we can use an even more efficient method to break the encrypted advertisement in The Times: we look for a word in the ciphertext that has a distinctive letter pattern. The best candidate we can find is ‘wtbsfdoesksjd’ – it contains the same letter (‘s’) at the fourth, ninth and eleventh position, while the sixth and the last letter (‘d’) are the same, too.
All other letters in this word are different. CrypTool 2 provides a tool that searches for words with a given repetition pattern in a large database. For ‘wtbsfdoesksjd’ we receive only one hit: ADVERTISEMENT. This is certainly a common word in a newspaper ad.
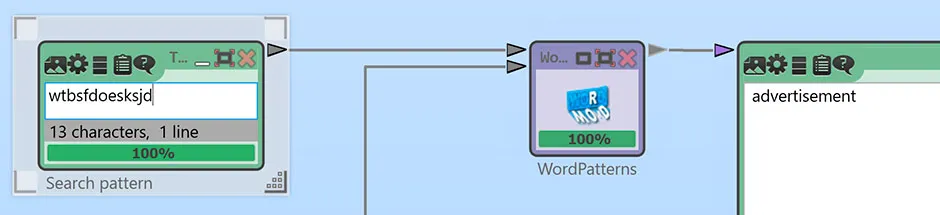
Assuming that ADVERTISEMENT is correct, we can determine the meaning of the following letters:
Plaintext: A D E I M N R S T V
Ciphertext: W T S O K J F E D B
This enables us to identify or guess more words. For instance, the first word, HFOBWDS, represents ?R?VATE, which can be solved as PRIVATE. This tells us that the ciphertext letters H and O stand for P and I. The ciphertext ‘wtbous’ decrypts to ADVI?E, which should be ADVICE (it can’t be ADVISE, as the S is already attributed to another letter) and shows that ciphertext ‘u’ corresponds with plaintext C. We have identified enough letters now that we should be able to decipher more words. In the end, we get the plaintext given above.
This advertisement reads as a message from a woman to her husband who has left her. We will probably never learn who created it and why – after all, this ad was published 150 years ago. However, from a codebreaker’s point of view the mystery is solved.
That was not very difficult, was it? In the course of this book, you will get to know more complicated encryption methods along with more sophisticated techniques for breaking them.
How do I know what kind of encryption I am dealing with?
Breaking a ciphertext usually requires knowing what kind of encryption method has been used. Apart from cipher-breaking methods, we therefore introduce in this book several cipher-detecting techniques. Finding out which cipher was used can vary from being quite simple to very difficult. It is helpful to know that most messages encountered in practice have been encrypted with one of about a dozen methods that can usually be distinguished from each other with some analysis.
If you want to identify a particular cipher without reading the whole book, the following paragraphs will give you some guidance.
If the encrypted text you want to solve looks like this:
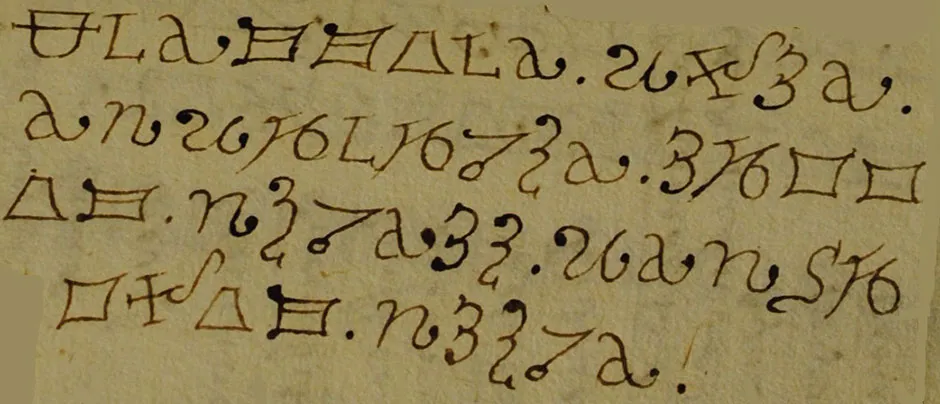
...or like this...
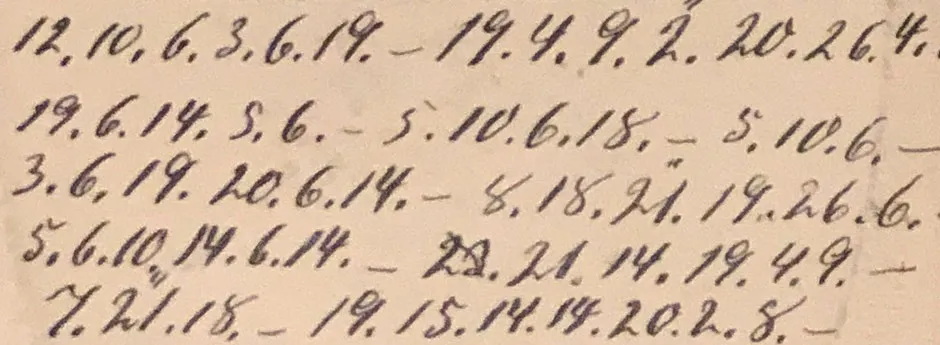
...or like this...

...or like this...
SIAA ZQ LKBA. VA ZOA RFPBLUAOAR!
...it is likely a substitution cipher.
If the cryptogram you want to solve looks like this:

...it is most likely a code or nomenclator.
If your ciphertext looks like this:

...it is likely a turning grille encryption.
If the encrypted text you want to solve looks like this:

...or like this...

...it is probably an abbreviation cipher.
If the encrypted text you want to solve looks like this:
218.57 106.11 8.93 17.61 223.64 146.7 244.53 224.21 20 192.5 160.19 99.39 No. 8 251.70 1 223.64 58.89 151.79 226.69 8.93 40.12 149.9 248.101 167.12 252.35 12.31 135.100 149.9 145.76 225.53 212.25 20 241.6 222.22 78.45 12.31 66.28 252.33 158.33 6.65 20 2 11.50 142.37 223.87 12.31 142.37 105.33 142.37 157.20 58.62 133.89 250.86.
...it may be a dictionary code or book cipher.
If you are dealing with five-letter groups...

...there are several possibilities, the most likely being a code, a transposition cipher, a digraph substitution or a machine cipher.
Want to learn more? We have full chapters on each of the above types in Codebreaking: A Practical Guide.
Codebreaking: A Practical Guide (£16.99, Hachette) is out now.
